Hoe Teken Je Een Raaklijn Aan Een Kromme?
Raaklijn Tekenen En Snelheid Berekenen
Keywords searched by users: hoe teken je een raaklijn
Hoe teken je een raaklijn?
Een raaklijn is een rechte lijn die precies één punt gemeen heeft met een kromme, zoals een cirkel of een grafiek van een functie. Het tekenen van een raaklijn kan nuttig zijn bij het bepalen van de steilheid van een curve op een bepaald punt of om de richting van een bewegend object te bepalen. In dit artikel zullen we bespreken hoe je een raaklijn kunt tekenen en hoe je de formule van een raaklijn kunt opstellen. We zullen ook praten over de raaklijnmethode, het vinden van een vergelijking van een raaklijn, raakpunten en tangentpunten, en de richtingscoëfficiënt.
Hoe stel je de formule van een raaklijn op?
Om de formule van een raaklijn op te stellen, heb je een punt op de curve en de richting van de raaklijn nodig. Laten we een voorbeeld nemen om dit te illustreren. Stel dat we de raaklijn aan de functie f(x) = x^2 willen vinden op het punt (2, 4).
Om de richting van de raaklijn te bepalen, kunnen we de afgeleide van de functie berekenen. In dit geval is de afgeleide van f(x) gelijk aan f'(x) = 2x.
Vervolgens kunnen we de richtingscoëfficiënt van de raaklijn berekenen door de afgeleide in te vullen voor x in het punt waar de raaklijn het curvepunt raakt. In dit geval is de richtingscoëfficiënt gelijk aan m = f'(2) = 2(2) = 4.
Nu hebben we een punt en een richtingscoëfficiënt, dus kunnen we de formule van de raaklijn opstellen met behulp van de punt-hellingsvorm. De punt-hellingsvorm is y – y1 = m(x – x1), waarbij (x1, y1) het gegeven punt is en m de richtingscoëfficiënt.
In ons voorbeeld wordt de formule van de raaklijn y – 4 = 4(x – 2). We kunnen deze vergelijking vereenvoudigen om de formule te krijgen: y = 4x – 4.
Het vinden van een vergelijking van een raaklijn
Om een vergelijking van een raaklijn te vinden, hebben we een punt op de curve en de richting van de raaklijn nodig. Dit kan worden bereikt met behulp van de afgeleide van de functie op het punt waar de raaklijn het curvepunt raakt.
Laten we als voorbeeld de functie f(x) = 2x^3 nemen en de raaklijn opstellen op het punt (1, 2). De afgeleide van f(x) is f'(x) = 6x^2.
Om de richtingscoëfficiënt te berekenen, vullen we x = 1 in de afgeleide in: m = f'(1) = 6(1)^2 = 6.
Nu hebben we een punt (1, 2) en een richtingscoëfficiënt m = 6. Met behulp van de punt-hellingsvorm kunnen we de formule van de raaklijn opstellen: y – 2 = 6(x – 1). Vereenvoudigen geeft y = 6x – 4.
Op deze manier kunnen we de vergelijking van een raaklijn vinden door een bekende functie te differentiëren en de richtingscoëfficiënt te berekenen.
Raaklijnmethode
De raaklijnmethode is een methode om de richtingscoëfficiënt van een curve op een bepaald punt te bepalen. Deze methode kan worden gebruikt om de richting van een object te bepalen dat een bepaalde curve volgt.
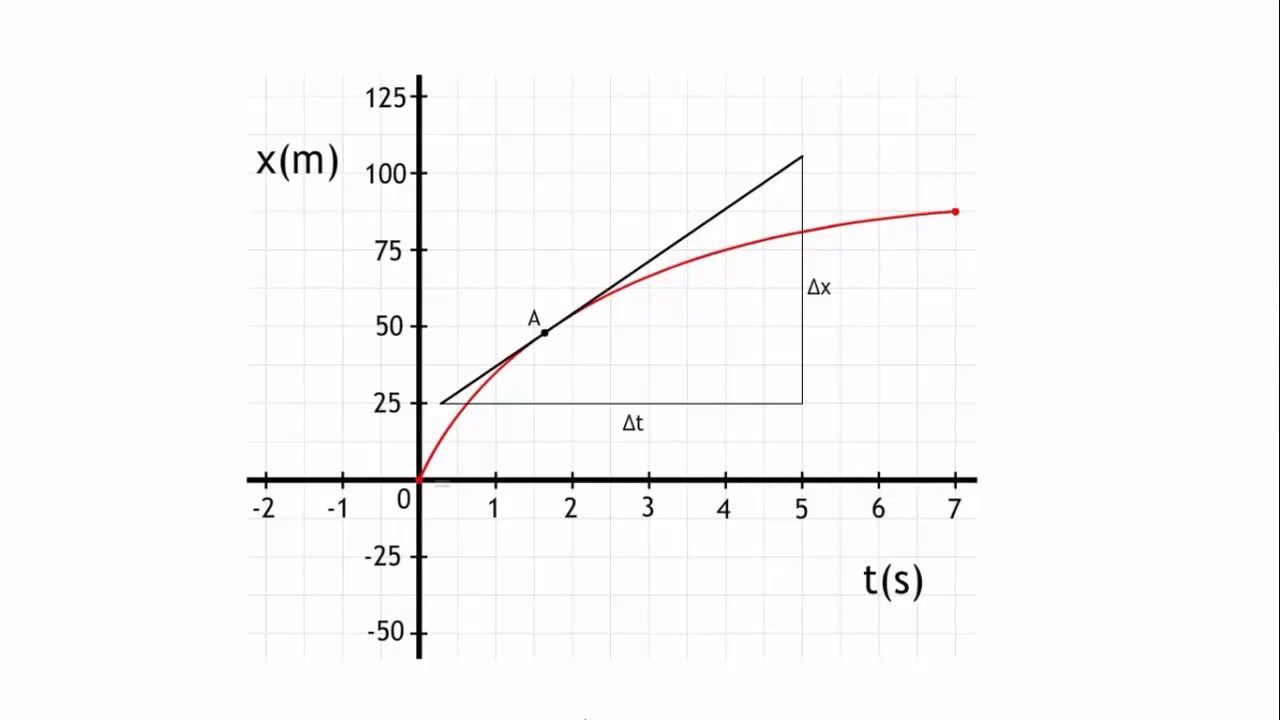
Om de raaklijnmethode toe te passen, moeten we het interval van verandering van x (Δx) en het interval van verandering van y (Δy) bepalen. Vervolgens delen we Δy door Δx om de richtingscoëfficiënt te berekenen.
Laten we een voorbeeld nemen om dit te verduidelijken. Stel dat een object een curve volgt en zich verplaatst van punt A naar punt B. We willen de richtingscoëfficiënt op punt A berekenen.
We meten de verandering in x (Δx) en de verandering in y (Δy) van punt A naar punt B. Stel dat Δx gelijk is aan 3 en Δy gelijk is aan 6.
Om de richtingscoëfficiënt te berekenen, delen we Δy door Δx: m = Δy / Δx = 6 / 3 = 2.
De richtingscoëfficiënt m = 2 geeft aan dat de curve op punt A een steilte heeft van 2. Dit betekent dat het object op dat punt met een snelheid van 2 eenheden in de y-richting beweegt voor elke eenheid die het in de x-richting beweegt.
De raaklijn aan een cirkel
Een raaklijn aan een cirkel is een rechte lijn die precies één punt gemeen heeft met de cirkel en loodrecht staat op de lijn die het middelpunt van de cirkel verbindt met het raakpunt.
Om de raaklijn aan een cirkel te tekenen, hebben we het middelpunt en de straal van de cirkel nodig. Laten we aannemen dat het middelpunt van de cirkel (h, k) is en de straal r.
De vergelijking van de cirkel is gegeven door (x – h)^2 + (y – k)^2 = r^2.
We kunnen de helling van de raaklijn berekenen door de afgeleide van de vergelijking van de cirkel te nemen en deze in te vullen voor x op het punt waar de raaklijn het raakpunt heeft. De helling van de raaklijn is gelijk aan -1 / m, waarbij m de afgeleide is.
Daarna kunnen we de formule van de raaklijn opstellen gebruikmakend van de punt-hellingsvorm met behulp van het punt van raaklijn. Het punt waar de raaklijn het raakpunt heeft, kan worden berekend door de straal r af te trekken van het middelpunt van de cirkel.
Op deze manier kunnen we een raaklijn aan een cirkel vinden en tekenen.
Raakpunten en tangentpunten
Een raakpunt (of tangentpunt) is het punt waar een raaklijn de curve raakt en slechts één gemeenschappelijk punt heeft met de curve.
Bij het tekenen van een raaklijn aan een curve, is het belangrijk om het raakpunt te identificeren om de formule van de raaklijn correct op te stellen.
Om het raakpunt te vinden, moeten we de vergelijking van de curve oplossen met de vergelijking van de raaklijn. Dit kan resulteren in een punt dat het raakpunt vertegenwoordigt.
Het raakpunt kan worden gebruikt om de formule van de raaklijn op te stellen met behulp van de punt-hellingsvorm, zoals eerder besproken.
Richtingscoëfficiënt
De richtingscoëfficiënt (of helling) is een waarde die aangeeft hoe steil een rechte lijn is. Het is de verhouding tussen de verandering in de y-coördinaat en de verandering in de x-coördinaat.
De formule voor de richtingscoëfficiënt is m = Δy / Δx, waarbij Δy de verandering in de y-coördinaat is en Δx de verandering in de x-coördinaat.
De richtingscoëfficiënt geeft de verhouding weer tussen de stijging en de horizontale verplaatsing van een lijn. Een positieve richtingscoëfficiënt geeft een stijgende lijn aan, terwijl een negatieve richtingscoëfficiënt een dalende lijn aangeeft. Een richtingscoëfficiënt van 0 geeft een horizontale lijn aan.
De richtingscoëfficiënt kan worden gebruikt om de steilheid van een curve te bepalen op een bepaald punt. Dit kan handig zijn bij het tekenen van raaklijnen aan grafieken van functies.
Met behulp van de richtingscoëfficiënt kunnen we ook de formule van een raaklijn opstellen zoals besproken in eerdere secties.
FAQs:
1. Wat is een raaklijn?
Een raaklijn is een rechte lijn die precies één punt gemeen heeft met een kromme, zoals een cirkel of een grafiek van een functie. Het raakpunt is het punt waar de raaklijn de kromme raakt.
2. Hoe stel je de formule van een raaklijn op?
Om de formule van een raaklijn op te stellen, heb je een punt op de curve en de richting van de raaklijn nodig. Bereken de richtingscoëfficiënt door de afgeleide van de functie in te vullen voor x op het gegeven punt. Gebruik de punt-hellingsvorm om de formule van de raaklijn op te stellen.
3. Wat is de raaklijnmethode?
De raaklijnmethode is een methode om de steilheid van een curve op een bepaald punt te bepalen. Het maakt gebruik van de verhouding tussen de veranderingen in x en y om de richtingscoëfficiënt te berekenen.
4. Wat is een raakpunt?
Een raakpunt, ook wel een tangentpunt genoemd, is het punt waar een raaklijn de curve raakt en slechts één gemeenschappelijk punt heeft met de curve.
5. Wat is de richtingscoëfficiënt?
De richtingscoëfficiënt is de waarde die aangeeft hoe steil een rechte lijn is. Het is de verhouding tussen de verandering in de y-coördinaat en de verandering in de x-coördinaat. Het kan worden gebruikt om de steilheid van een curve op een bepaald punt te berekenen en om de formule van een raaklijn op te stellen.
Categories: Top 25 Hoe Teken Je Een Raaklijn
Hoe Maak Je Een Raaklijn?
Hoe Vind Je Een Raaklijn?
Wat Is De Raaklijnmethode?
Aggregeren 27 hoe teken je een raaklijn






See more here: c1.chewathai27.com
Learn more about the topic hoe teken je een raaklijn.
- Hoe stel je de formule van een raaklijn op? – Mr. Chadd
- 2. Het vinden van een vergelijking van een raaklijn – WisFaq!
- Raaklijnmethode – Natuurkunde Uitgelegd
- Raaklijn – Wikipedia
- Richtingscoëfficiënt – Wikipedia
- raaklijn aan cirkel – H. Hofstede
See more: c1.chewathai27.com/category/herstelrubriek